Simplifying Boolean Equations with Karnaugh Maps

In this series, I will comprehensively cover all topics related to K Maps. The content will include the basic representation, rules for grouping, examples, and the Quine Mccluskey Minimization technique.

• The Karnaugh Map, also known as the K Map, is a method used for simplifying Boolean expressions.
• It was introduced by Maurice Karnaugh in 1953 and is built on the basis of Gray code, a binary numeral system in which two successive values differ in only one binary bit.
• The process involves transferring the Boolean results from a truth table into a two-dimensional grid, where the cells are ordered in gray code, and each cell position represents a combination of input conditions.
• The K-map can be used in two forms: Sum of Products (SOP) and Product of Sums (POS), depending on the problem’s requirements. For SOP, we place 1s at the respective cells, while for POS, we put 0s at the respective cells.
• Let’s consider a 2-Variable Karnaugh Map (K-Map):
  To determine the total number of cells in the K-Map, we use the formula 2^n, where n is the number of variables. In this case, with 2 variables, we have 2² = 4 cells.
• The diagram below illustrates a 2-variable K-Map with variables A and B, each capable of taking values 0 and 1. We can represent A as Abar when its value is 0, and as A when its value is 1, and similarly for variable B.

• Each cell is identified by its corresponding row and column values. For instance, Cell 1 has the values A̅ and B̅ (00), so it is in the 0th position. Similarly, Cell 2 has the values A̅ and B (01), placing it in the 1st position. Cell 3 has the values A and B̅ (10), making it the 2nd position, and Cell 4 has the values A and B (11), making it the 3rd position. This method allows us to determine the positions of the cells accurately.
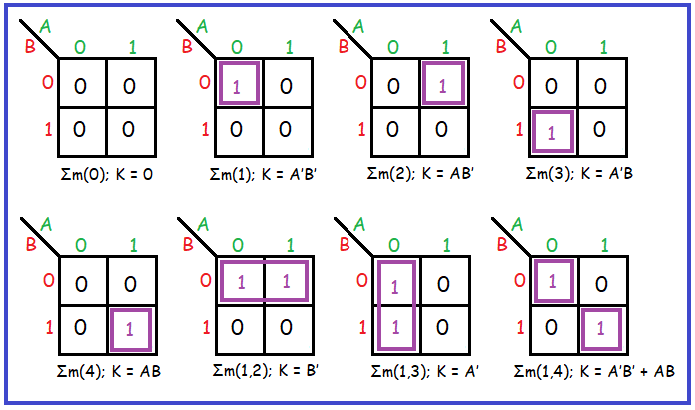
• Now, let’s discuss using the K-Map to simplify a Boolean equation, for example, Y (A, B) = Σm(0, 3). To apply this equation to the K-Map, we place 1s at the 0th and 3rd positions. In this case the kmap will look as follows:

A minterm represents the most minimal expression of the mapped variables in a Boolean equation.

• The following are all the possible 2- variable 2x2 Karnaugh maps:

• Now, consider 3 variable K Map:
  The total number of cells for 3 variables will be 2³ which is 8 cells.
• The below diagram shows the K Map for 3 variables.
  Here, for AB we will have 2-bit grey code combination sequence. Similar to 2 variable kmap 3 variable kmap will also have positions based on values of A, B and C.

• Now, let’s discuss using the K-Map to simplify a Boolean equation, for example, Y (A, B, C) = Σm(0, 1, 4, 6). To apply this equation to the K-Map, we place 1s at the 0th, 1st, 4th and 6th positions. In this case the kmap will look as follows:

• For the 4 variable kmap:
  The total number of cells for 4 variables will be 2⁴ which is 16 cells.
• The below diagram shows the K Map for 4 variables.
  Here, for AB and CD we will have 2-bit grey code combination sequence. Similar to 2 variable kmap 4 variable kmap will also have positions based on values of A, B, C and D.

• Now, let’s discuss using the K-Map to simplify a Boolean equation, for example, Y (A, B, C, D) = Σm(1, 5, 9, 12, 14). To apply this equation to the K-Map, we place 1s at the 1st, 5th, 9th, 12th and 14th positions. In this case the kmap will look as follows:

In my upcoming blog, I will delve into the topic of Rules for Grouping and Forming a Boolean Equation. Stay tuned for more! :)

Like, Share and Follow me if you like my content.
Thank You.