Mastering Verilog: Implementing Logic Gates.

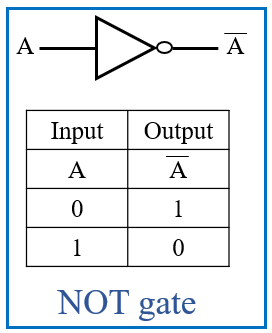
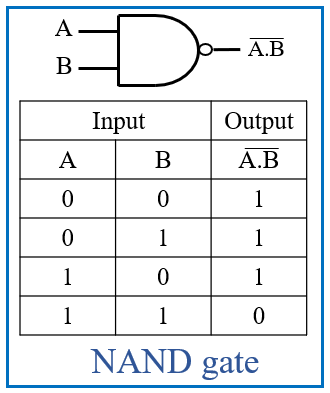
Welcome to the world of digital design! In this blog post, we’ll dive into Verilog code examples for essential logic gates used in digital circuits. Understanding how to implement these gates is foundational for building complex digital systems.

For a detailed insight into how these logic gates operate, including their truth tables, click on the link provided below:
Logic Gates

Below, you’ll find Verilog code implementations for various logic gates using two different methods:
1. Behavioral Modeling: Describes the logic behavior using `always @(*)` blocks.
2. Dataflow Modeling: Describes the logic using continuous assignments (`assign`).

1. AND Gate

Behavioral Modeling:

module AND_Gate(input wire a, input wire b, output reg y);
 always @(*) begin
 y = a & b;
 end
endmodule

Dataflow Modeling:

module AND_Gate(input wire a, input wire b, output wire y);
 assign y = a & b;
endmodule

2. OR Gate

Behavioral Modeling:

module OR_Gate(input wire a, input wire b, output reg y);
 always @(*) begin
 y = a | b;
 end
endmodule

Dataflow Modeling:

module OR_Gate(input wire a, input wire b, output wire y);
 assign y = a | b;
endmodule

3. NAND Gate

Behavioral Modeling:

module NAND_Gate(input wire a, input wire b, output reg y);
 always @(*) begin
 y = ~(a & b);
 end
endmodule

Dataflow Modeling:

module NAND_Gate(input wire a, input wire b, output wire y);
 assign y = ~(a & b);
endmodule

4. NOR Gate

Behavioral Modeling:

module NOR_Gate(input wire a, input wire b, output reg y);
 always @(*) begin
 y = ~(a | b);
 end
endmodule

Dataflow Modeling:

module NOR_Gate(input wire a, input wire b, output wire y);
 assign y = ~(a | b);
endmodule

5. XOR Gate

Behavioral Modeling:

module XOR_Gate(input wire a, input wire b, output reg y);
 always @(*) begin
 y = a ^ b;
 end
endmodule

Dataflow Modeling:

module XOR_Gate(input wire a, input wire b, output wire y);
 assign y = a ^ b;
endmodule

6. XNOR Gate

Behavioral Modeling:

module XNOR_Gate(input wire a, input wire b, output reg y);
 always @(*) begin
 y = ~(a ^ b);
 end
endmodule

Dataflow Modeling:

module XNOR_Gate(input wire a, input wire b, output wire y);
 assign y = ~(a ^ b);
endmodule

Conclusion

These Verilog code snippets demonstrate two ways of implementing logic gates:

- Behavioral Modeling is more abstract and suitable for complex logic, using `always` blocks to describe how the logic should behave.
- Dataflow Modeling is closer to the gate-level, where continuous assignments (`assign`) directly describe how the inputs connect to the outputs.

Experiment with both methods to understand their behavior and use them as building blocks for creating sophisticated digital designs.

Happy Coding!

Unveiling the World of Logic Gates: The Building Blocks of Digital Circuits

 

• Logic gates serve as fundamental building blocks that execute logical operations on binary inputs, resulting in binary outputs. These gates form the foundation of digital circuits, playing a pivotal role in the processing and manipulation of digital information.
• A Truth table provides a systematic representation of potential input combinations alongside their respective outputs for a given logic gate or logical expression. In this table, each row signifies a distinct set of input values, with the corresponding output determined by the behavior of the logic gate.
• Following are the types of Logic gates:

1. AND
2. OR
3. NOT
4. NOR
5. NAND
6. XOR
7. XNOR

• Let’s delve into the specifics of each logic gate:

1] AND Gate:

An AND gate features a single output and multiple inputs. When all inputs are high (1), the output is high (1). The Boolean logic is expressed as Y = A.B for two inputs, A and B. The AND gate is represented by the following symbol and truth table:

2] OR Gate:

The OR gate accepts two or more inputs and produces one output. If at least one input is high (1), the output is high (1). The mathematical expression for a two-input OR gate is Y = A + B. The OR gate symbolizes its logic, where the output is high when any input is high. The OR gate is represented by the following symbol and truth table:

3] NOT Gate:

The NOT gate is a single-input, single-output gate. It produces the inverse of its input, and its Boolean equation is Y = A’. It is also known as an inverter. The NOT gate is represented by the following symbol and truth table:

4] NOR Gate:

A NOR gate is formed by combining an OR gate followed by a NOT gate. The output is high only when all inputs are low (0). The Boolean statement for the NOR gate is Y=(A+B)’ if there are two inputs A and B. It can serve as a universal gate for implementing OR, AND, and NOT.

5] NAND Gate:

A NAND gate is essentially a Not gate followed by an AND gate. The output is low only when none of the inputs is low (0). If there are two inputs A and B, the Boolean expression for the NAND gate is Y=(A.B)’. The NAND gate is known as a universal gate because it may be used to implement the AND, OR, and NOT gates.

6] XOR Gate:

The Exclusive-OR or ‘Ex-OR’ gate is a digital logic gate that accepts more than two inputs but only outputs one value. If any of the inputs is 1 the output of the XOR Gate is 1. If both inputs are ‘1’ the output is ‘0’ If both inputs are ‘0’ the output is ‘0’.
The Boolean equation for the XOR gate is Y=A’.B+A.B’ if there are two inputs A and B. The XOR gate is represented by the following symbol and truth table:

7] XNOR:

The Exclusive-NOR or ‘EX-NOR’ gate is a digital logic gate that accepts more than two inputs but only outputs one. If both inputs are ‘1’ the output of the XNOR Gate is ‘1’ If both inputs are ‘0’ the output is ‘1’ If one of the inputs is 0’ the output is ‘0’. If there are two inputs A and B, then the XNOR gate’s Boolean equation is: Y=A.B+A’B’. The truth table shows that its outputs are based on NOR gate logic. The XNOR gate is represented by the following symbol and truth table:

Exploring the intricate world of logic gates has unveiled the fundamental building blocks of digital circuits. We’ve navigated through the functions of AND, OR, NOT, NOR, NAND, XOR, and XNOR gates, unraveling their symbolic representations, Boolean equations, and truth tables. Understanding these essential components is key to mastering digital circuit design. As we close this exploration, let the knowledge of logic gates empower your journey into the realm of digital electronics and circuitry.

Like, Share and Follow me if you like my content.
Thank You.