Mastering the Language of Digital Electronics: An Introduction to Boolean Algebra and DeMorgan’s Laws

 

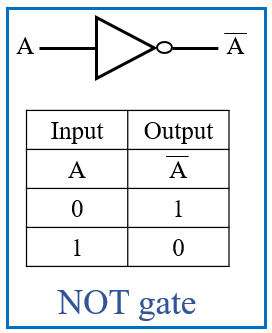
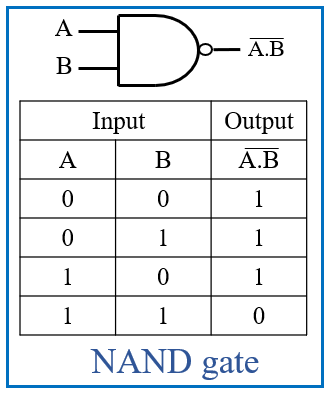
• In the world of digital electronics, where the magic of computation happens, lies a fundamental concept that serves as the building blocks for all operations: Boolean equations.
• These equations, rooted in the mathematics of Boolean algebra, govern the behavior of digital circuits, enabling the creation of complex systems from simple components. In this blog post, we’ll delve into the realm of Boolean equations.
• Boolean algebra deals with binary variables and logic operations. The variables take on the values of either 0 or 1, representing false and true, respectively. Boolean equations express logical relationships between these variables using operators such as AND, OR, and NOT.
• The basic operators in Boolean algebra are:

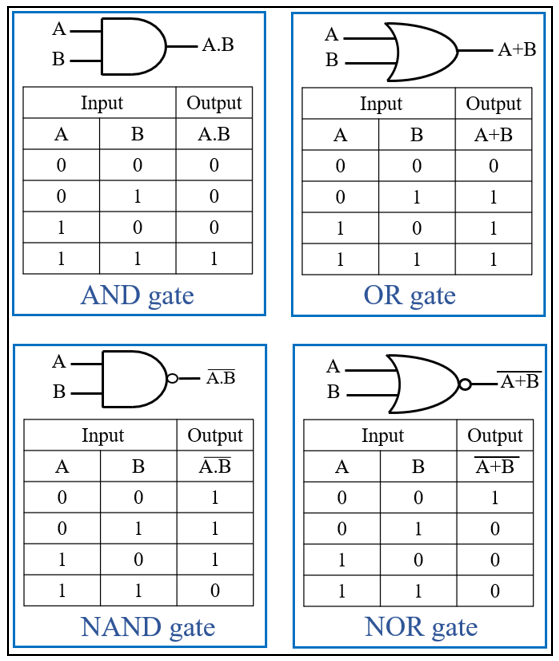
1. AND (·): This operator returns true (1) only if both inputs are true.
2. OR (+): This operator returns true (1) if at least one input is true.
3. NOT (‘): This operator returns the opposite value of the input.

• Boolean Algebra operates under several fundamental laws that govern the manipulation and simplification of Boolean expressions. These laws provide a systematic way to analyze and optimize digital circuits. Let’s explore some of the key laws in Boolean algebra:

1. Identity Laws:
   1] Identity Law for OR: The OR operation with one operand being true always results in true.
   A + 1 = 1
   2] Identity Law for AND: The AND operation with one operand being false always results in false.
   A · 0 = 0
2. Domination Laws:
   1] Domination Law for OR: If one operand of an OR operation is true, the result is true regardless of the other operand.
   A + 0 = A
   2] Domination Law for AND: If one operand of an AND operation is false, the result is false regardless of the other operand.
   A · 1 = A
3. Idempotent Laws:
   1] Idempotent Law for OR: ORing a variable with itself is the same as the variable itself.
   A + A = A
   2] Idempotent Law for AND: ANDing a variable with itself is the same as the variable itself.
   A · A = A
4. Commutative Laws:
   1] Commutative Law for OR: The order of operands in an OR operation does not affect the result.
   A + B = B + A
   2] Commutative Law for AND: The order of operands in an AND operation does not affect the result.
   A · B = B · A
5. Associative Laws:
   1] Associative Law for OR: The grouping of operands in an OR operation does not affect the result.
   (A + B) + C = A + (B + C)
   2] Associative Law for AND: The grouping of operands in an AND operation does not affect the result.
   (A · B) · C = A · (B · C)
6. Distributive Laws:
   1] Distributive Law for OR over AND: Distributing an OR operation over an AND operation.
   A + (B · C) = (A + B) · (A + C)
   2] Distributive Law for AND over OR: Distributing an AND operation over an OR operation.
   A · (B + C) = (A · B) + (A · C)
7. Demorgans Laws

• A famous mathematician DeMorgan invented the two most important laws which play on important role in solving various boolean algebra expressions.
• It basically describes the amazing relationship between logic gates and their corresponding relations.
• These 2 laws deal with 4 logic gates: AND, OR, NOR and NAND.
• Let us consider each law one by one:
• But before we explore these laws, let’s refresh our memory with the truth tables of the AND, OR, NAND, and NOR gates:

1] Demorgan’s First Law:
According to the 1st Law, the complement of AND operation is equal to the OR operation of the complement of that variable. This can be summerized in the below figure and truth table.

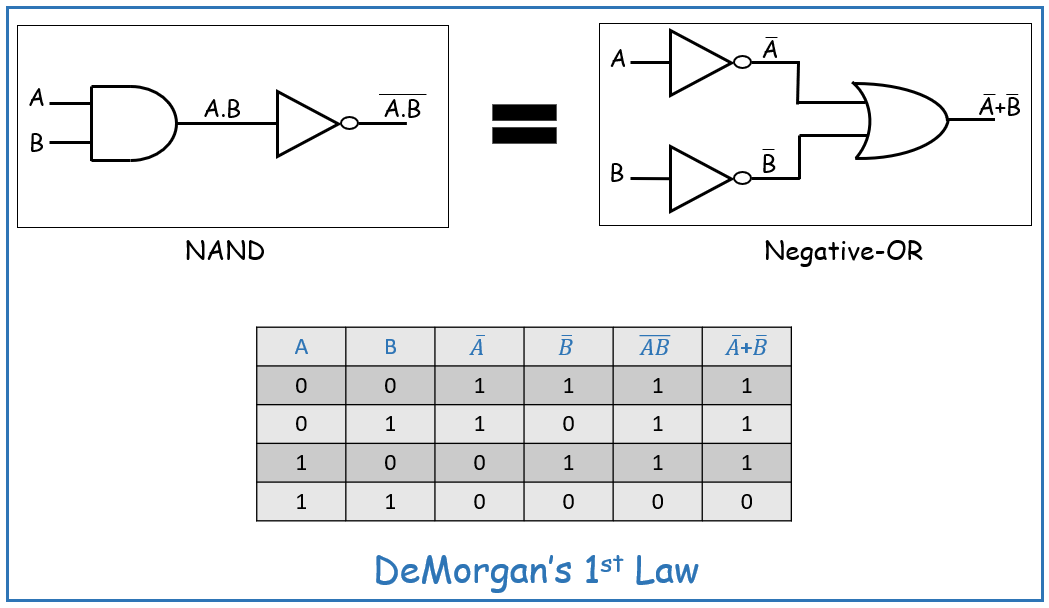
Here from the truth table you can observe that for each combination of values of A and B the output values of operation (A.B) bar and (A)bar + (B)bar are equal. 

2] Demorgan’s Second Law:
According to the 2st Law, the complement of OR operation is equal to the AND operation of the complement of that variable. This can be summerized in the below figure and truth table. 

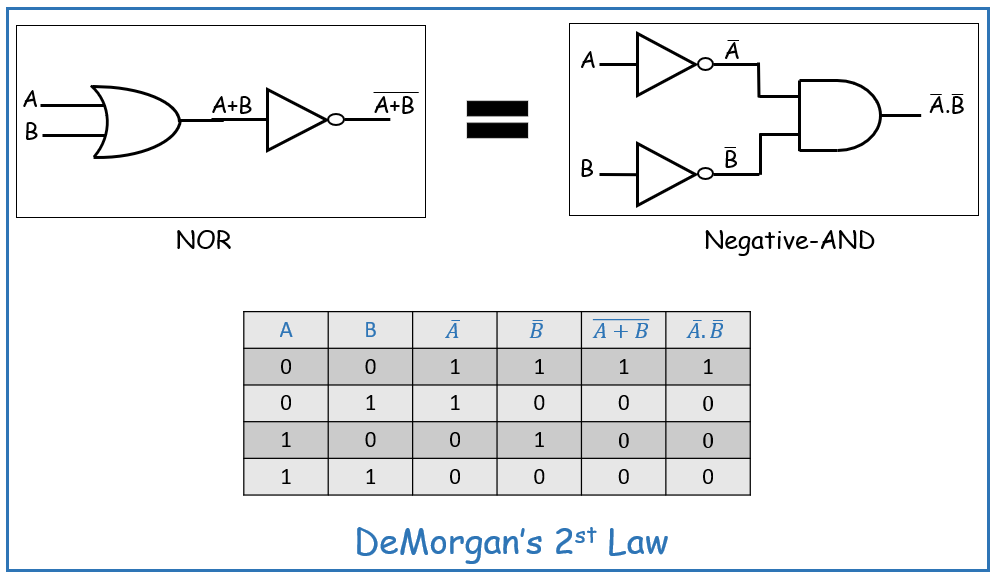
Here from the truth table you can observe that for each combination of values of A and B the output values of operation (A+B) bar and (A)bar . (B)bar are equal. 

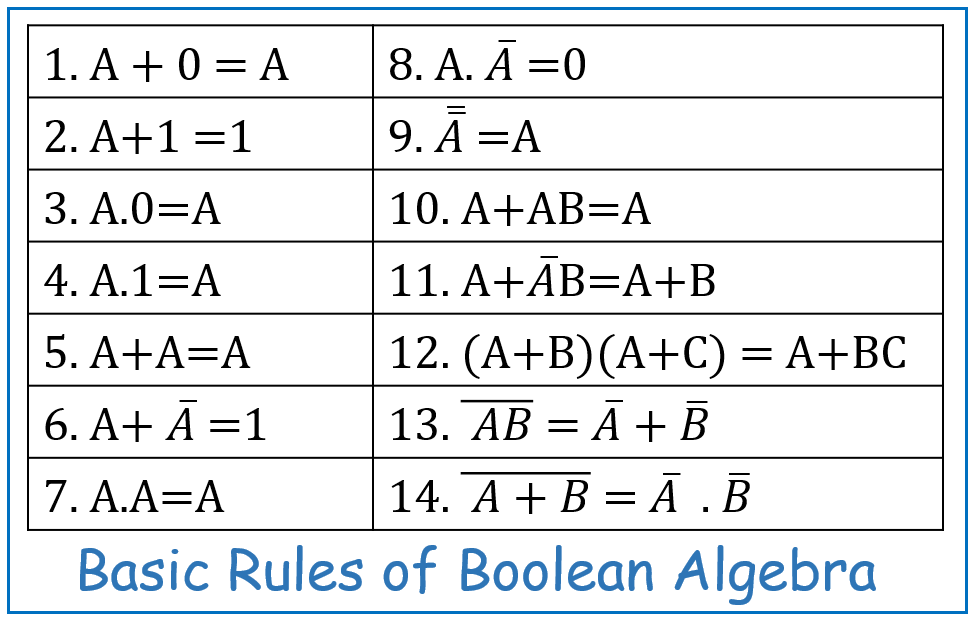
• Hence, below figure summerizes the rules of boolean algebra: 

• Now let us consider few examples and see how these two laws help us evalute the output easily: 

Example 1:

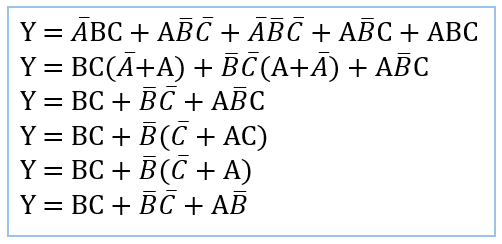
Example 2:

Boolean equations are the language of digital electronics, enabling engineers to design and analyze complex systems with precision and efficiency. By understanding the basic principles of Boolean algebra and mastering the manipulation of Boolean equations, one can unlock the full potential of digital circuitry. Whether you’re designing a basic logic gate or a sophisticated microprocessor, Boolean equations are your indispensable tool for success in the world of digital electronics.

Like, Share and Follow me if you like my content.
Thank You.

Unveiling the World of Logic Gates: The Building Blocks of Digital Circuits

 

• Logic gates serve as fundamental building blocks that execute logical operations on binary inputs, resulting in binary outputs. These gates form the foundation of digital circuits, playing a pivotal role in the processing and manipulation of digital information.
• A Truth table provides a systematic representation of potential input combinations alongside their respective outputs for a given logic gate or logical expression. In this table, each row signifies a distinct set of input values, with the corresponding output determined by the behavior of the logic gate.
• Following are the types of Logic gates:

1. AND
2. OR
3. NOT
4. NOR
5. NAND
6. XOR
7. XNOR

• Let’s delve into the specifics of each logic gate:

1] AND Gate:

An AND gate features a single output and multiple inputs. When all inputs are high (1), the output is high (1). The Boolean logic is expressed as Y = A.B for two inputs, A and B. The AND gate is represented by the following symbol and truth table:

2] OR Gate:

The OR gate accepts two or more inputs and produces one output. If at least one input is high (1), the output is high (1). The mathematical expression for a two-input OR gate is Y = A + B. The OR gate symbolizes its logic, where the output is high when any input is high. The OR gate is represented by the following symbol and truth table:

3] NOT Gate:

The NOT gate is a single-input, single-output gate. It produces the inverse of its input, and its Boolean equation is Y = A’. It is also known as an inverter. The NOT gate is represented by the following symbol and truth table:

4] NOR Gate:

A NOR gate is formed by combining an OR gate followed by a NOT gate. The output is high only when all inputs are low (0). The Boolean statement for the NOR gate is Y=(A+B)’ if there are two inputs A and B. It can serve as a universal gate for implementing OR, AND, and NOT.

5] NAND Gate:

A NAND gate is essentially a Not gate followed by an AND gate. The output is low only when none of the inputs is low (0). If there are two inputs A and B, the Boolean expression for the NAND gate is Y=(A.B)’. The NAND gate is known as a universal gate because it may be used to implement the AND, OR, and NOT gates.

6] XOR Gate:

The Exclusive-OR or ‘Ex-OR’ gate is a digital logic gate that accepts more than two inputs but only outputs one value. If any of the inputs is 1 the output of the XOR Gate is 1. If both inputs are ‘1’ the output is ‘0’ If both inputs are ‘0’ the output is ‘0’.
The Boolean equation for the XOR gate is Y=A’.B+A.B’ if there are two inputs A and B. The XOR gate is represented by the following symbol and truth table:

7] XNOR:

The Exclusive-NOR or ‘EX-NOR’ gate is a digital logic gate that accepts more than two inputs but only outputs one. If both inputs are ‘1’ the output of the XNOR Gate is ‘1’ If both inputs are ‘0’ the output is ‘1’ If one of the inputs is 0’ the output is ‘0’. If there are two inputs A and B, then the XNOR gate’s Boolean equation is: Y=A.B+A’B’. The truth table shows that its outputs are based on NOR gate logic. The XNOR gate is represented by the following symbol and truth table:

Exploring the intricate world of logic gates has unveiled the fundamental building blocks of digital circuits. We’ve navigated through the functions of AND, OR, NOT, NOR, NAND, XOR, and XNOR gates, unraveling their symbolic representations, Boolean equations, and truth tables. Understanding these essential components is key to mastering digital circuit design. As we close this exploration, let the knowledge of logic gates empower your journey into the realm of digital electronics and circuitry.

Like, Share and Follow me if you like my content.
Thank You.