In the world of digital systems, data transmission and processing depend on the conversion and manipulation of binary data. Just as encoders convert information from one format into another, decoders serve the reverse function: they translate encoded data back into its original form. Decoders are essential in numerous applications, from simple digital circuits to complex communication systems. In this blog, we will explore what decoders are, how they work, and where they are used.
What is a Decoder?
A decoder is a combinational logic circuit that converts coded inputs into coded outputs. More specifically, a decoder takes a binary input (often in the form of n inputs) and produces an output based on the input combination. The output is typically an active signal on one of its multiple output lines, corresponding to the binary input pattern.
In simple terms, while an encoder compresses data into a smaller number of bits, a decoder expands those bits back to their original form, recovering the original information.
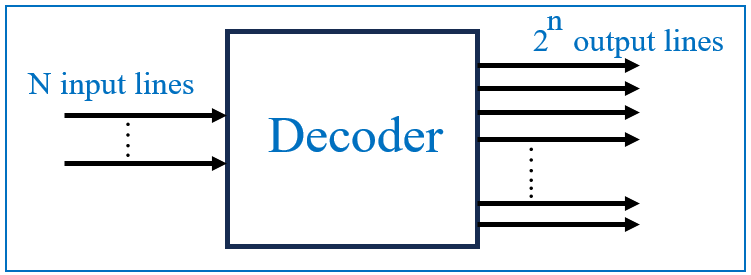
A basic decoder performs the reverse operation of an encoder. It takes an n-bit binary input and provides up to 2^n unique output lines. This feature makes decoders highly useful in applications where a specific output needs to be activated based on a binary input code.
For example, a 2-to-4 decoder has two input lines (A0, A1) and four output lines (Y0, Y1, Y2, Y3). It converts the 2-bit binary input into a unique active output line. Each combination of the input corresponds to one of the output lines being activated, while the others remain inactive.
Types of Decoders
Decoders come in various configurations based on the number of inputs and outputs. The most common types include:
- 2-to-4 Decoder: As described above, a 2-bit input produces four possible outputs.
- 3-to-8 Decoder: A 3-bit input results in eight possible outputs, often used in memory address decoding.
- 4-to-16 Decoder: Expanding further, a 4-bit input activates one of sixteen outputs, commonly used in microprocessors for selecting memory locations or devices.
In some applications, decoders may also include enable inputs that allow or block the decoding function.
Working Principle of a Decoder
The function of a decoder can be understood through its basic logic structure. Consider a 2-to-4 decoder, one of the simplest forms of decoders. It takes a 2-bit binary input and activates one of four output lines based on the input combination:
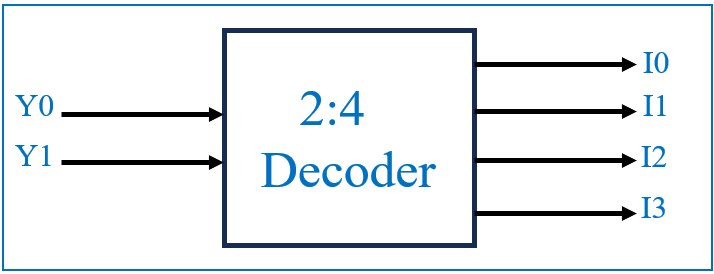
- Input: 00 → Output Line 0 is active
- Input: 01 → Output Line 1 is active
- Input: 10 → Output Line 2 is active
- Input: 11 → Output Line 3 is active
Each output is mapped to a specific input combination, typically using AND gates. The truth table of the 2-to-4 decoder demonstrates this operation:

Thus, depending on the binary value of the input, only one output line is active at any given time.
Block Diagram and Logic Circuit Explanation
The block diagram below shows a basic 2:4 decoder with two inputs (Y0, Y1) and four outputs (I0, I1, I2, I3):
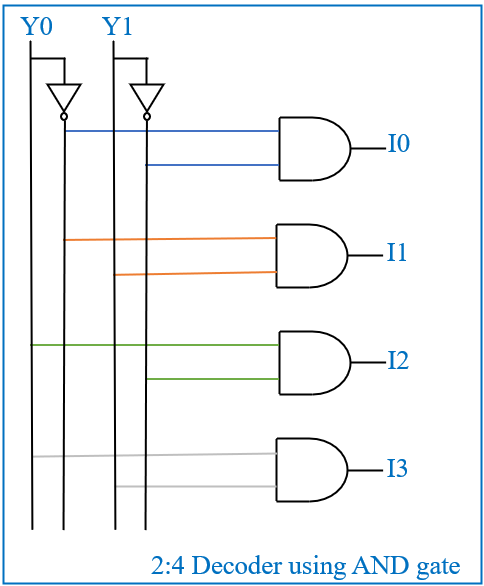
This decoder activates a specific output based on the combination of the input values. The internal circuit uses AND gates and NOT gates to realize the function. Each output is connected to a specific combination of inputs, as shown in the logic diagram below:
In this logic circuit:
- I0 is activated when both Y1 and Y0 are low (00), utilizing a NOT gate on both inputs before sending them to the AND gate.
- I1 is activated when Y1 is low and Y0 is high (01).
- I2 is activated when Y1 is high and Y0 is low (10).
- I3 is activated when both Y1 and Y0 are high (11).
The following equations describe each output:
- I0 = ~Y1 & ~Y0 (Active when both inputs are 00)
- I1 = ~Y1 & Y0 (Active when the input is 01)
- I2 = Y1 & ~Y0 (Active when the input is 10)
- I3 = Y1 & Y0 (Active when both inputs are 11)
Verilog Code for 2-to-4 Decoder
Here’s a simple Verilog code for a 2-to-4 binary decoder:
module decoder_2to4 (
input wire A0, // First input bit
input wire A1, // Second input bit
output wire Y0, // Output line 0
output wire Y1, // Output line 1
output wire Y2, // Output line 2
output wire Y3 // Output line 3
);
// Logic for the decoder using continuous assignment
assign Y0 = ~A1 & ~A0; // Active when A1A0 is 00
assign Y1 = ~A1 & A0; // Active when A1A0 is 01
assign Y2 = A1 & ~A0; // Active when A1A0 is 10
assign Y3 = A1 & A0; // Active when A1A0 is 11
endmoduleApplications of Decoders
Decoders are used extensively in digital electronics and communication systems. Some common applications include:
- Memory Address Decoding: Decoders are used in microprocessors and memory systems to select specific memory locations. A decoder decodes the binary address provided by the CPU, activating the corresponding memory location for reading or writing data.
- Seven-Segment Display: A special type of decoder converts binary or BCD (Binary-Coded Decimal) data into signals that light up specific segments of a seven-segment display, representing numbers.
- Data Demultiplexing: Decoders can act as demultiplexers, routing a single input signal to one of many output lines based on the input address.
- Instruction Decoding: In CPUs, decoders are used to interpret machine code instructions and activate the appropriate circuitry to execute each command.
- Communication Systems: Decoders play a vital role in converting encoded signals back into their original form, enabling correct data reception.
Conclusion
Decoders are indispensable in digital electronics, facilitating the process of translating coded information back into a usable form. From enabling memory selection in computers to powering seven-segment displays, decoders are everywhere in modern technology. By understanding the principles behind decoders, you gain deeper insights into how data is processed and transmitted in digital systems.
Whether you’re building a simple logic circuit or designing complex communication protocols, understanding decoders is essential to mastering digital electronics.