LTspice is a SPICE-based analog circuit simulation software developed by Analog Devices (originally by Linear Technology). It is the most widely used SPICE simulator in the industry. LTspice features schematic capture for designing electronic circuits, an advanced SPICE-based simulator, and a waveform viewer for analyzing simulation results. It supports various circuit analysis types, including transient, noise, AC, DC, DC transfer function, and DC operating point simulations, along with Fourier analysis. Additionally, it can calculate component heat dissipation and generate efficiency reports. While it does not generate printed circuit board (PCB) layouts, it allows netlist export for use in PCB design software.
It is commonly used in analog circuit design for simulating amplifiers, filters, signal conditioning circuits, and sensor interfaces. Mixed-signal circuits involving analog and digital components can also be tested within LTspice. Many universities and research institutions use LTspice for teaching circuit design concepts and conducting advanced research in analog/RF circuit design, power systems, and semiconductor device modeling. It is a preferred tool due to its accuracy, free availability, and extensive component library.
Installation process
You can download the software from the link below. It is completely free, easy to install, and ready to use within minutes.
LTSpice Download Link
Designing Our First Circuit: Voltage Divider in LTspice
Let’s begin by designing our first circuit, a voltage divider. Below is the basic schematic, which consists of a voltage source and two resistors in series.
Step 1: Create a New Schematic
- Open LTspice and start a new schematic (automatically named “Draft 1”).

Step 2: Placing Components
- The toolbar at the top contains essential components.
- To place a resistor, select it from the toolbar or press “R” on your keyboard. Press “Esc” to deselect.
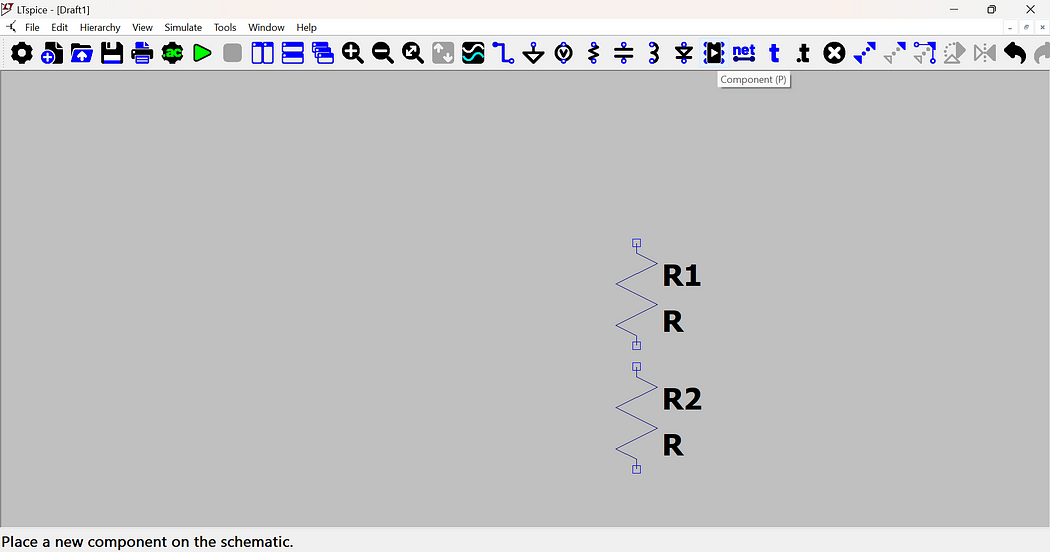
- For a voltage source, go to the Components menu, scroll to the end, and select “Voltage”.

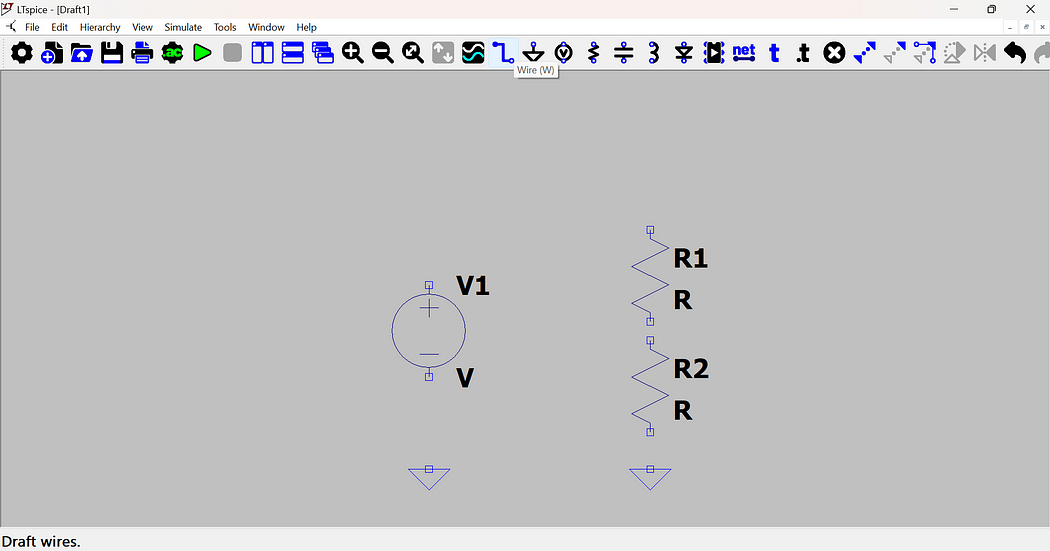
- Finally, add a ground connection.

- Use the wire tool to connect the components. One of LTspice’s best features is that wires automatically link components when dragged through them.
Step 3: Assigning Component Values
- To set values for resistors and voltage:
- Hover over a component, right-click, and enter the desired values in the pop-up window.

- You can also add text labels to your schematic for clarity.


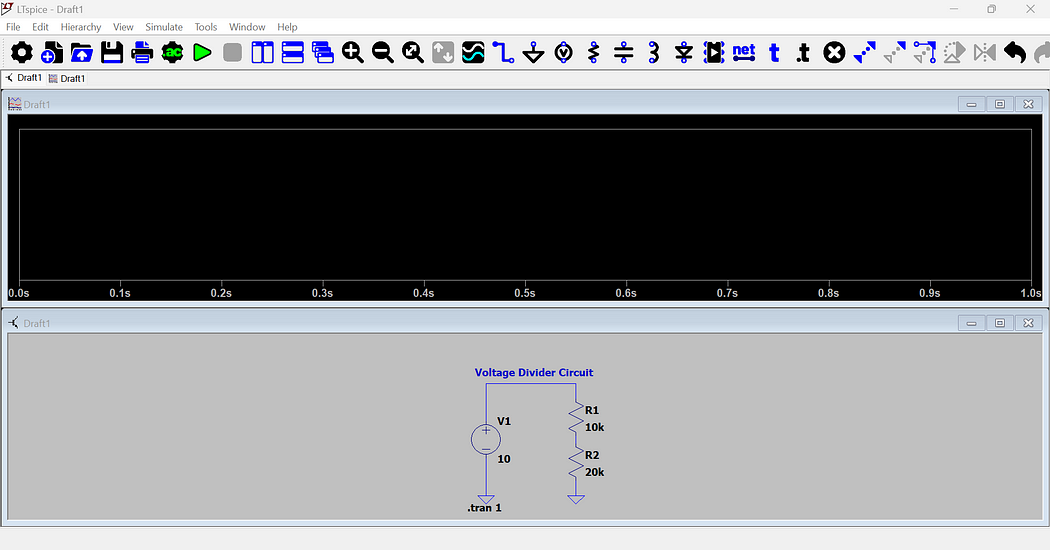
- Once done, your complete circuit should resemble the following diagram.
Step 4: Running the Simulation
- To simulate the circuit, set the stop time to 1 second for a basic analysis.
- Keep the remaining settings default for a simple simulation.

- Now that we have designed our voltage divider circuit, let’s measure different values across different components in LTspice.
Step 5: Measuring Voltage
- Move your mouse cursor over the circuit schematic. You will see a red probe icon when hovering over a node.
- Click on the node where you want to measure the voltage. The corresponding voltage waveform will be displayed in the simulation window.
- In our case, you can probe the middle node between R1 and R2 to measure the divided voltage.

Measure Voltage Difference (Across Two Nodes)
- To measure the voltage difference between two nodes:
- Hold Ctrl while clicking on one node, then click on another node.
- This will plot the voltage difference between the two selected points.
- Example:
- If you click on the top of R1 (where V1 is applied) and then on the bottom of R2 (ground), you will see the total applied voltage.

Additional Tips:
- The measured voltage appears as a graph in the simulation window.
- Move the cursor over the waveform to see exact values at different time points.
- To adjust the voltage scale, click on the voltage axis in the simulation window and manually set the range.
- In this case, you can adjust the scale from 12V to 0V for better visualization of the waveform.

Step 6: Measuring Current
- In LTspice, current is measured through a component, not at a single node like voltage.
- Move the mouse cursor over a resistor (R1 or R2) or the voltage source (V1).
- You will see a current probe icon (clamp symbol) appear.
- Click on the component (e.g., R1 or R2) where you want to measure the current.
- The corresponding current waveform will appear in the simulation window.
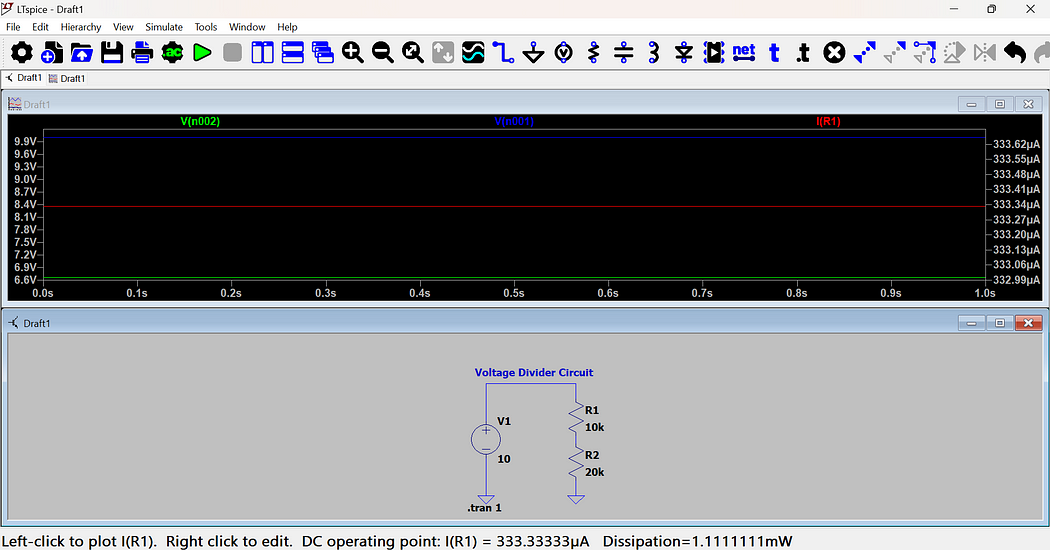
Step 7: Measuring Current through the Voltage Source
- To measure the total circuit current, hover over the voltage source (V1).
- When the current probe appears, click on it. This will show the current supplied by the source.

Step 8: Adjusting the Current Scale
- If needed, click on the current axis in the simulation window and adjust the range for better visualization.
- You can also right-click on the waveform and select “Add Cursors” for precise measurements.
Step 9: How to Remove Unwanted Waveforms
If you have selected multiple components for measurement and want to remove some waveforms from the simulation window, follow these steps:
Method 1: Right-Click and Delete
- Move the cursor over the waveform (voltage or current) you want to remove.
- Right-click on the waveform.
- Select “Delete This Trace” from the menu.
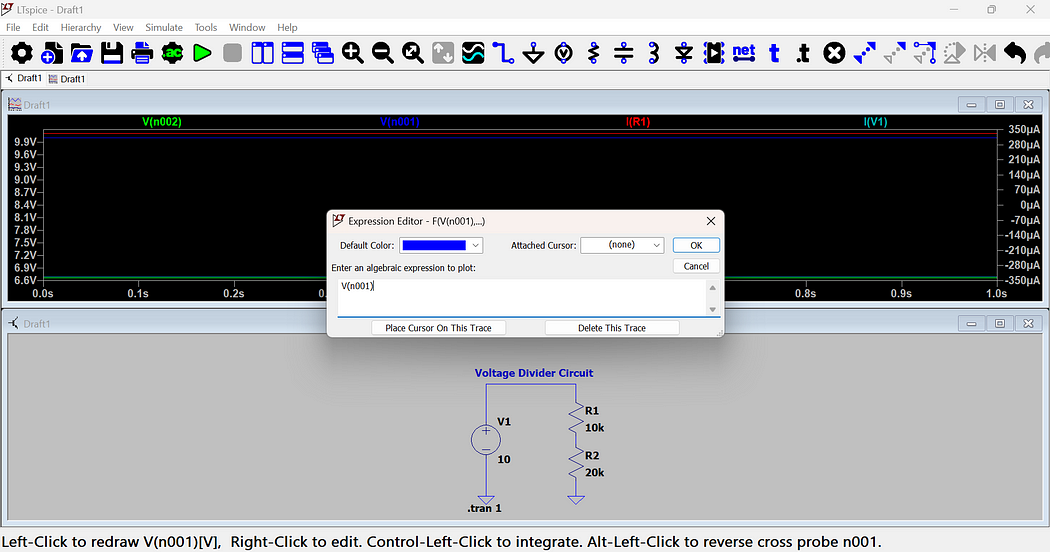

Step 10: Measuring Power
- Move your cursor over the component whose power you want to measure.
- Hold the “Alt” Key — The cursor will change to a power symbol (a probe with a watt symbol).
- Click on the Component — LTspice will automatically display the power waveform in the simulation window.
- Adjust the Scale (Optional) — If needed, right-click on the waveform and adjust the axis scale for better visualization.

Step 11: How to Add a Label in LTspice
Adding labels in LTspice helps in identifying nodes easily, especially when dealing with complex circuits.
Steps to Add a Label:
- Select the Label Tool — Click on the “net” tool.
- Enter the Label Name — A small window will pop up. Type the desired label name (e.g., “Output”) and click OK.
- Place the Label — Click at the node where you want to add the label.
- Connect with a Wire (if needed) — If the label isn’t directly at the node, use the wire tool to connect it properly.
- Verify the Label — Once added, the label will be visible, and LTspice will recognize it as a named node in the simulation results.

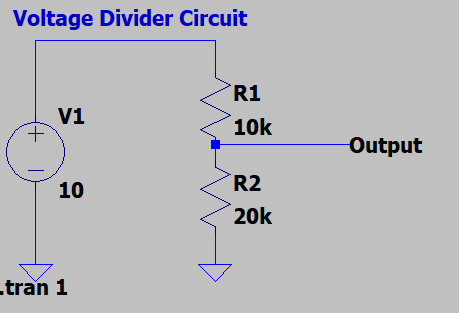
Step 12: How to View Only a Specific Waveform in LTspice
If multiple waveforms are displayed and you want to see only the current through R1, follow these steps:
- Double-Click on the Component — Locate R1 in the schematic and double-click on it.
- Only the Current Through R1 Will Be Displayed — LTspice will remove all other waveforms and display only the selected component’s current.
- To Bring Back Other Waveforms — If you need to view additional signals, you will have to reselect them by probing the circuit again.
Step 13: Performing Operations on Waveforms
We can also double the output voltage and see it by going to the Expression Editor.


In this way, we can perform different mathematical operations like:
- Addition
- Subtraction
- Multiplication
- Custom functions on signals
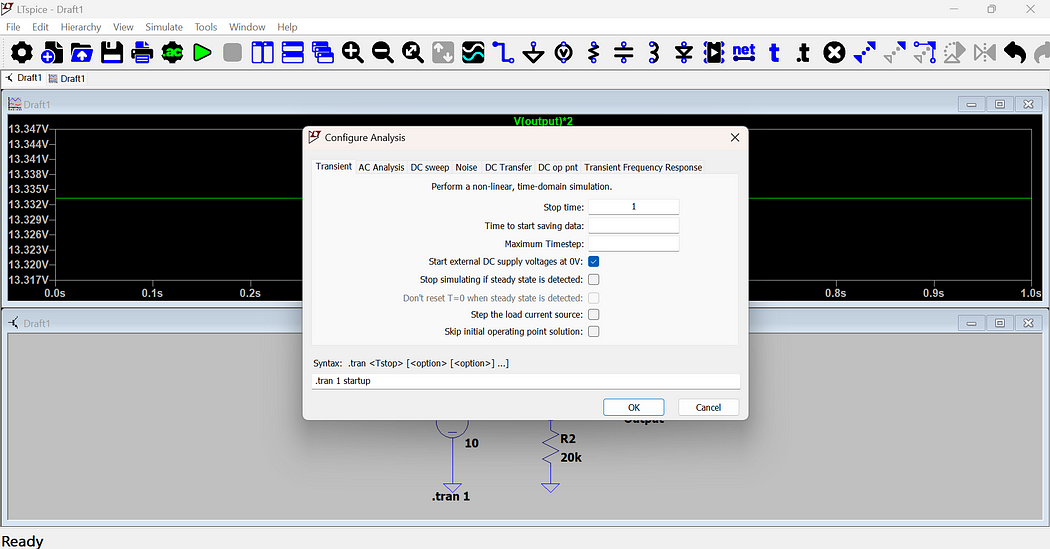
Step 14: How to Start with a DC Supply That Ramps from 0V to 10V in LTspice
If you want the DC supply to start from 0V and gradually ramp up to 10V, follow these steps:
- Go to Simulate → Configure Analysis
- Select the “Transient” Tab
- Check the Option — Enable “Start external DC supply voltages at 0V”
- Run the Simulation — Click OK and run the simulation to see the voltage ramp-up.
- Control the Area to View the Ramp-Up Waveform — Click and drag over the desired area to zoom in and focus on the ramp-up.

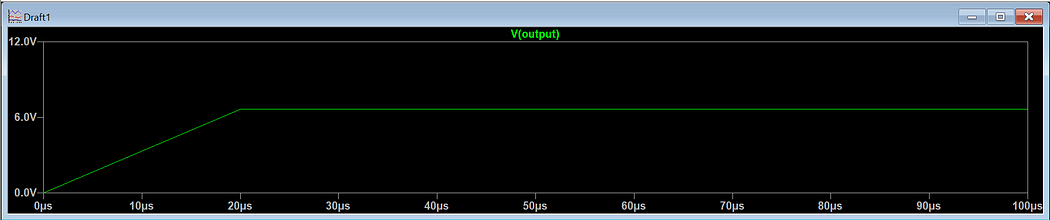
This method is useful when simulating circuits that require a smooth power-up behavior! 🚀📈
In this tutorial, we covered the installation of LTspice and designed a simple voltage divider circuit. We learned how to place components, assign values, run simulations, and measure voltage, current, and power. These are fundamental steps in circuit simulation, forming the basis for more advanced designs.
✔️ Try designing your own circuit in LTspice and share your experience in the comments!
✔️ If you found this guide helpful, share it with others who might benefit!
✔️ Follow me for more LTspice tutorials and circuit design tips!