Simplifying Boolean Equations with Karnaugh Maps — Part: 1 Grouping Rules

 In my previous blogs, we have seen what are kmaps and basic structure of 2,3, 4 variable Kmap. Now let us see the Grouping Rules for cells in Kmaps.

• Now to form a Boolean equation we need to group these cells.
  So, the basic rules are as follows:

1. We need to group the cells with value 1 and may not include any cell containing zero.
2. Groups may be horizontal, vertical but not diagonal.
3. Groups must contain 1, 2, 4, 8, or in general 2n cells.
4. Group should be as large as possible.
5. Groups can overlap eachother.
6. Opposite or corner cells can be grouped.
7. Groups may wrap around the table. The leftmost cell in a row may be grouped with the rightmost cell and the top cell in a column may be grouped with the bottom cell.
8. There should be as few groups as possible, as long as this does not contradict any of the previous rules.

• Let us consider each rule one by one:

1] We need to group the cells with value 1 and may not include any cell containing zero:
For grouping in k map, we cannot group cell with 0 and 1 together but can group cells with only value 1.

2] Groups may be horizontal, vertical but not diagonal:

3] Groups must contain 1, 2, 4, 8, …. ,2n cells:

4] Group should be as large as possible:
As you can see in the above diagram, we need to group the cells as large as possible. Note that the grouping in 1st image doesn’t break any Boolean law but it is not sufficiently minimal.

5] Groups can overlap each other:
So, to form minimal groups we can overlap the groups as shown below:

6] Opposite or corner cells can be grouped:

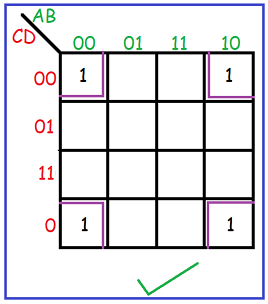
7] Groups may wrap around the table. The leftmost cell in a row may be grouped with the rightmost cell and the top cell in a column may be grouped with the bottom cell:

8] There should be as few groups as possible, as long as this does not contradict any of the previous rules:

In this way using above rules we can group the cells and form a Boolean equation.

In the next blog, let us form a Boolean equation using these grouping Rules. So, Stay Tuned! :)

Like, Share and Follow me if you like my content.
Thank You.