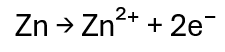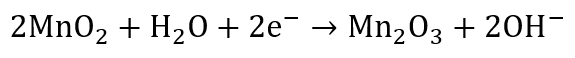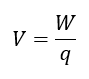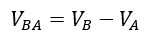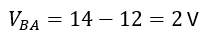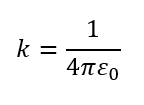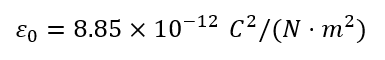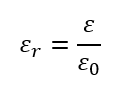Explore Our Topics!

Check out the extensive list of topics we discuss: 

1. Tech and AI Blogs
2. Communication Protocols:
   - USB 
   - RS232 
   - Ethernet 
   - AMBA Protocol: APB, AHB and ASB 
   - UART, I2C AND SPI
3. Important concepts in VLSI:
   - Designing a Chip? Here Are the 12 Important Concepts You Need to Know
   - Metastability 
   - Setup time and Hold time
   - Signal Integrity and Crosstalk effect
   - Skews and Slack 
   - Antenna Effect
4. Semiconductor Memories
   
5. Analog vs Digital Electronics
6. Most Frequently Asked Questions in VLSI
7. VLSI and Semiconductor Nuggets: Bite-Sized knowledge for Enthusiasts
8. Common Acronyms in VLSI and Semiconductor Industry
9. Transistors:
   - BJT
   - JFET
   - MOSFET
   - CMOS
   - Transmission Gate CMOS
   - Dynamic CMOS
10. Sequential Circuits:
    - Registers
    - Counters
    - Latches
    - Flip Flops
11. FPGA:
    - ASIC vs FPGA
    - FPGA Insights: From Concept to Configuration
    - Full-Custom and Semi-Custom VLSI Designs: Pros, Cons and differences
    - From Theory to Practice: CMOS Logic Circuit Design Rules Made Easy with Examples
12. CMOS Fabrication:
    - CMOS Fabrication
    - Twin-Tub CMOS Technology
13. Combinational Circuits
    - Logic Gates 
    - Boolean Algebra and DeMorgan's Law 
    - Multiplexer (MUX) and Demultiplexer (DEMUX) 
    - Half Adder
    - Full Adder
    - Half Subtractor
    - Full Subtractor
    - Encoders
    - Decoder
14. Analog Electronics
    - Atoms: the Foundation of Electronics
    - Electrons, Protons and Neutrons 
    - Electron Shells, Subshells and Energy Ordering
    - Energy Band: The Key to Conductors, Semiconductors, Insulators and Dielectrics
    - Intrinsic and Extrinsic Semiconductors
    - Electric Charge and Permittivity
    - Electric Potential and Voltage
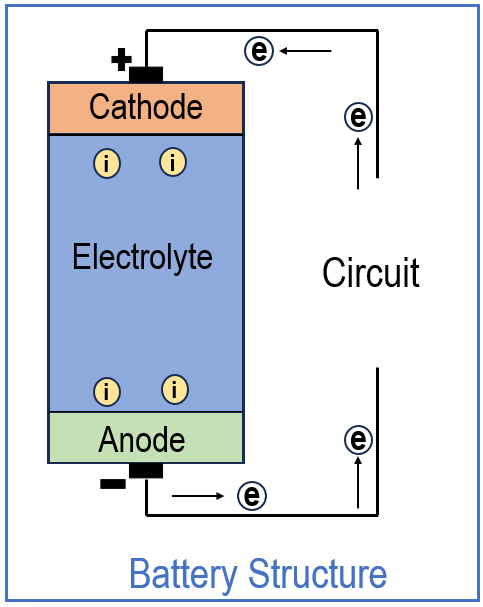
    - Basic Structure and Working of Battery
    - Understanding Resistor
    - Understanding Resistivity
    - Understanding Capacitor and Capacitance
    - Understanding Inductors and Inductance
    - Understanding Reactance
    - Understanding Impedance
    - Understanding Resonance
    - OPAMP
    - Inverting and Non-inverting Amplifiers
    - Characteristics of OPAMP
    - OPAMP Application: Adder, Subtractor, Differentiator, and More!  
    - Filters
    - Hard Disk Drives Explained
    - Passive Components: Capacitors and Resistors Explained
    - LTSpice Tutorial 1: Installation and First Circuit Simulation
15. Verilog
    - Verilog Datatypes
    - Comments, Numeral Formats and Operators
    - Modules and Ports
    - assign, always and initial keywords
    - Blocking and Non-Blocking Assignments
    - Conditional Statements
    - Looping Statements
    - break and continue Statement
    - Tasks and Functions
    - Parameter and generate
    - Verilog Codes
16. System Verilog: 
    - Disable fork and Wait fork.
    - Fork and Join.
17. Project on Intel Quartus Prime and Modelsim:
    - Vending Machine Controller
18. Xilinx Vivado Projects
    1)VHDL
    - Counters using Testbench code
    - Flip Flops using Testbench code
    - Logic Gates using Testbench code
    - Full Adder using Half Adder and Testbench code
    - Half Adder using Testbench code
    2)Verilog
    - Logic Gates using Testbench code
    - Counters using Testbench code
    - Full Adder using Half Adder and Testbench code
    - Half Adder using Testbench code
19. VLSI Design Flow:
    - Design Flow in VLSI
    - Y chart or Gajski Kuhn Chart
20. Projects on esim:
    - Step-by-Step guide on how to Design and Implement a Full Adder using CMOS and sky130nm PDK
    - Step-by-Step guide on how to Design and Implement a Half Adder using CMOS and sky130nm PDK
    - Step-by-Step guide on how to Design and Implement a 2:1 MUX using CMOS and sky130nm PDK
    - Step-by-Step guide on how to Design and Implement a Mixed-Signal Circuit of 2:1 Multiplexer
21. IoT based project:
    - Arduino
    - Step-by-Step guide on how to Interface Load Cell using Arduino
22. Kmaps:
    - Simplifying Boolean Equations with Karnaugh Maps - Part:2 Implicants, Prime Implicants and Essential Prime Implicants. 
    - Simplifying Boolean Equations with Karnaugh Maps - Part:1 Grouping Rules.
    - Simplifying Boolean Equation with Karnaugh Maps.

Understanding Resonance in AC Circuits — When Reactances Cancel Out

In AC circuits, frequency plays a crucial role in deciding how current flows. At one special frequency, the effects of inductors and capacitors perfectly balance each other, leading to a powerful phenomenon called resonance.

In this blog, we’ll understand what resonance is, why it happens, and how it can be visualized using a practical RLC circuit simulation.

---

⚡ Resonance

Resonance in an AC circuit is the condition at which the inductive reactance (Xₗ) becomes equal to the capacitive reactance (X꜀), causing them to cancel each other out. At resonance, the circuit behaves purely resistive, and the current becomes maximum.

To understand resonance, you must understand impedance and reactance.

---

🔌 What Is Impedance?

In AC circuits, current and voltage change direction continuously.

So, opposition to current is not just resistance (R). There are two more components:

• Inductive reactance (Xₗ) — comes from inductors

• Capacitive reactance (X꜀) — comes from capacitors

The total opposition in an AC circuit is called Impedance (Z):

$$Z=\sqrt{R^2+(X_L-X_C{)}^2}$$

Where:

• $X_L = 2\pi f L$

• $X_C = \frac{1}{2\pi f C}$

Notice something important:

• Xₗ increases with frequency

• X꜀ decreases with frequency

But there is one special frequency where their effects cancel each other.

---

🎯 Resonance Condition

Resonance occurs where capacitive reactance equals inductive reactance:

$$X_L=X_{\mathrm{C<span\; style="font-family:\; georgia;"></span>}}$$

Substitute the formulas:

$$2\pi f_{0}L=\frac{1}{2\pi f_0\mathrm{C<span\; style="font-family:\; georgia;"></span>}}$$

Solving for frequency:

$$f_0 = \frac{1}{2\pi\sqrt{LC}}$$

This frequency is called the resonant frequency.

---

🔍 What Happens at Resonance?

At the resonant frequency $f_0$:

✔ Inductive reactance equals capacitive reactance

$$X_L-X_C=0$$

✔ Impedance becomes minimum

$$Z=R$$

The circuit behaves as if it has only resistance.

✔ Current becomes maximum

$$I=\frac{V}{\mathrm{R<span\; style="font-family:\; georgia;"></span>}}$$

✔ Voltage magnification occurs in L and C

Even though the net reactive effect is zero, energy continuously transfers between the inductor and capacitor:

• Inductor stores magnetic energy

• Capacitor stores electric energy

They keep exchanging energy, creating large voltages inside the circuit.

---

🧪 LTspice Simulation of Resonance

To visualize this phenomenon, a series RLC circuit was simulated in LTspice using the following values:

• R = 50 Ω

• L = 45 mH = 0.045 H

• C = 1.36 μF = 1.36 × 10⁻⁶ F

• AC source = 230 V

• AC sweep = 100 Hz to 2000 Hz

---

🔧 Circuit Explanation

The simulated circuit is a series RLC network.

All three components (R, L, and C) are connected one after another, and an AC source is applied across the combination.

The current through the resistor I(R1) is observed, which represents the current flowing through the entire series loop.

---

🧮 Resonant Frequency Calculation

Step 1: Multiply L and C

$$LC = 0.045 \times 1.36 \times 10^{-6}$$
$$LC = 6.12 \times 10^{-8}$$

---

Step 2: Square root of LC

$$\sqrt{LC} = \sqrt{6.12 \times 10^{-8}}$$ $$\sqrt{LC} = 2.472 \times 10^{-4}$$

---

Step 3: Multiply by $2\pi$

$$2\pi \times 2.472 \times 10^{-4}$$
$$2\pi \approx 6.283$$
$$2\pi \sqrt{LC}=0.001554$$

---

Step 4: Take reciprocal

$$f_0 = \frac{1}{0.001554}$$ $$f_0 \approx 643.7 \text{ Hz}$$
$$\boxed{f_0 \approx 644 \text{ Hz}}$$

---

📈 Verification from Simulation

At resonance:

• $X_L = X_C$

• Net reactance $X = 0$
  

• Impedance $Z = R = 50 \Omega$
  

Current becomes:

$$I = \frac{V}{R} = \frac{230}{50} = 4.6 \text{ A}$$

The simulation peak current is very close to 4.5–4.7 A, confirming perfect resonance behavior.

---

🔚 Conclusion

Resonance is a powerful condition in AC circuits where inductive and capacitive reactances cancel each other, leaving only resistance to oppose current flow. At this point, impedance is minimum and current reaches its maximum value.

Although the net reactance becomes zero, energy continuously oscillates between the magnetic field of the inductor and the electric field of the capacitor, leading to voltage magnification within the circuit. This phenomenon is the foundation of tuned circuits, filters, oscillators, and communication systems.

Understanding resonance completes the journey from resistance → reactance → impedance and opens the door to advanced AC circuit analysis.

Understanding Impedance — The Total Opposition in AC Circuits

In AC circuits, opposition to current is not as simple as resistance alone. When resistors, inductors, and capacitors work together, both magnitude and phase come into play.

This combined effect is called impedance, and it defines how AC circuits truly behave.

---

⚡ Impedance — The Total Opposition

Now, let’s combine everything.

When resistors, inductors, and capacitors are all connected in an AC circuit, the total opposition to current is called Impedance (Z).

Impedance includes both:

• Resistance (R) — which is constant and frequency-independent.

• Reactance (X) — which depends on frequency and causes phase shift.

---

📐 Definition of Impedance (Phasor Form)

When working with AC signals, both voltage and current are sinusoidal and can be represented as phasors — rotating vectors showing both magnitude and phase.

The true definition of impedance is based on this phasor relationship:

Z = Ṽ / Ĩ

where:

• Ṽ = voltage phasor (magnitude + phase)

• Ĩ = current phasor (magnitude + phase)

Thus, impedance is a complex ratio that expresses both:

• how strongly the circuit opposes current (magnitude), and

• how voltage and current are shifted relative to each other (phase difference).

From this relationship:

|Z| = |Ṽ| / |Ĩ|
∠Z = ∠Ṽ − ∠Ĩ

This means:

• The magnitude of impedance tells how much the circuit resists the flow of AC current.

• The phase angle (∠Z) shows whether voltage leads or lags current, and by how much.

---

❗ Important Clarification

Impedance is not simply the ratio of instantaneous or RMS values:

• ❌ Z = Vₚₑₐₖ / Iₚₑₐₖ

• ❌ Z = v(t) / i(t) (instantaneous values)

• ❌ Z = Vᵣₘₛ / Iᵣₘₛ — unless both are treated as phasors including phase information

✅ The correct and complete definition is:

Z = Ṽ / Ĩ

This phasor ratio accounts for both magnitude and phase, which is why impedance is a complex quantity, expressed as:

• Z = R + jX (rectangular form)

• Z = |Z| ∠ θ (polar form)

---

🧮 Magnitude of Impedance

The magnitude of impedance is given by:

Z = √(R² + X²)

Here, X can be:

• Positive → Inductive reactance (Xᴸ)

• Negative → Capacitive reactance (−Xᶜ)

In phasor form, impedance is written as:

Z = R + jX

where:

• j (or i) indicates a 90° phase shift

---

⚙️ Impedance of R, L, and C

• Resistor:
  Zᵣ = R (purely real, θ = 0°)

• Inductor:
  Zᴸ = jωL = j2πfL (purely imaginary, positive)

• Capacitor:
  Zᶜ = 1 / jωC = −j(1/ωC) (purely imaginary, negative)

So, for a circuit containing R, L, and C:

• Net reactance: X = Xᴸ − Xᶜ

• Total impedance: Z = R + j(Xᴸ − Xᶜ)

---

🎛️ Frequency Dependence

This is where the magic happens:

• Inductors: Reactance increases with frequency

• Capacitors: Reactance decreases with frequency

• Resistors: Unaffected by frequency

Because of this:

• Inductors and capacitors are frequency-dependent components

• Resistors are frequency-independent

This frequency-dependent behavior forms the basis of filters, oscillators, and resonant circuits — the heart of modern electronics.

---

🔚 Conclusion

Impedance is the complete description of how an AC circuit opposes current flow. It combines resistance, which dissipates energy, with reactance, which stores and returns energy through electric and magnetic fields.

While resistance determines how much current flows, impedance also tells us how voltage and current are phase-shifted, revealing the true dynamic nature of AC circuits. Its dependence on frequency is what enables filtering, tuning, resonance, and signal shaping in electronic systems.

Understanding impedance is a major step forward in electronics — it connects resistance, reactance, frequency, and phase into one powerful concept that brings AC circuits fully to life.

Understanding Reactance — Opposition to Change in AC Circuits

When we first learn about circuits, resistance feels like the only opposition to current. But as soon as we move into AC circuits, where voltage and current are constantly changing, a new concept comes into play — reactance.

In this blog, we’ll explore what reactance is, why it exists, and how it shapes the behavior of capacitors and inductors in AC systems.

---

⚡ What is Reactance?

When we first learn about circuits, we meet resistance — the opposition that limits how much current flows. But the moment we move from DC (Direct Current) to AC (Alternating Current), the story becomes much more interesting.

Here, the voltage and current are continuously changing, and this change introduces a new kind of opposition called Reactance.

Let’s explore what it really is, why it matters, and how it connects to a concept called Impedance — the total opposition in AC circuits.

In simple terms, reactance is the opposition that a capacitor or inductor offers to the flow of alternating current (AC).

It’s similar to resistance but with a key difference:

• Resistance opposes all current, whether AC or DC.

• Reactance only opposes changing current — the kind that goes up and down, like in AC.

When voltage and current are constantly varying, capacitors and inductors react to that change.

• Capacitors store energy in the electric field.

• Inductors store energy in the magnetic field.

Unlike resistors, these components don’t waste energy as heat. They temporarily store energy and return it to the circuit. This storage and return create a delay in current or voltage, and that delay is what we call reactance.

---

🔧 Why is Reactance Needed?

In an AC system, voltage and current are not steady — they continuously rise, fall, and even reverse direction.

This constant change interacts with capacitors and inductors, which try to “resist” or “delay” the change due to how they store energy.

• The inductor resists a change in current because it builds a magnetic field around itself.

• The capacitor resists a change in voltage because it builds up an electric field between its plates.

This time-dependent opposition is exactly what allows us to design filters, amplifiers, and tuned circuits — all of which depend on reactance.

---

⚖️ Reactance vs. Resistance

So, we don’t use the same word “resistance” for both because:

• Resistance dissipates energy as heat.

• Reactance stores and gives back energy.

Their effects on current and voltage are fundamentally different.

---

🌀 Inductive Reactance — Opposition from a Coil

An inductor is simply a coil of wire that stores energy in a magnetic field when current passes through it.

But when you try to change that current, the inductor resists (thanks to Lenz’s Law).

The fundamental relation for an ideal inductor is:

V = L (dI/dt)

Where:

• V = voltage across the inductor

• L = inductance (Henry)

• dI/dt = rate of change of current

This means the voltage depends on how quickly the current changes.

If the current changes fast, the voltage across the inductor becomes large.

Here’s what happens when AC is applied:

• The inductor initially resists the change — it takes time to build a magnetic field.

• The applied voltage goes into creating that magnetic field instead of immediately increasing current.

• Once the current flows, it continues even as voltage starts to fall, because the inductor releases its stored energy.

This delay means current lags behind voltage by 90° in a pure inductor.

Inductive reactance is given by:

Xₗ = 2πfL

Where:

• f = frequency (Hz)

• L = inductance (H)

So, as frequency increases, inductive reactance also increases.

That’s why:

• For DC (f = 0), Xₗ = 0 → acts like a short circuit.

• For high-frequency AC, Xₗ becomes very large → acts like an open circuit.

---

🔵 Capacitive Reactance — Opposition from a Capacitor

For a capacitor, the voltage and current relationship is:

i(t) = C (dv/dt)

Where:

• i(t) = current through the capacitor

• v(t) = voltage across the capacitor

• C = capacitance (Farad)

This equation shows that the current depends on how fast the voltage changes — not its actual value.

What really happens in AC:

• As voltage begins to rise, charges start moving instantly — current begins flowing immediately.

• It takes some time before enough charge accumulates for voltage to build up across the plates.

• Hence, current reaches its peak first — when voltage is changing fastest.

• Voltage reaches its maximum later — about a quarter cycle (90°) later.

Thus, current leads voltage by 90° in a pure capacitor.

Capacitive reactance is given by:

X꜀ = 1 / (2πfC)

So, as frequency increases, capacitive reactance decreases.

That’s why:

• Capacitors pass high-frequency signals easily.

• But they block DC (since f = 0 ⇒ X꜀ = ∞).

---

🔄 The Two Types of Reactance

If you observe closely, they’re complete opposites in nature:

• In an inductor, voltage leads current.

• In a capacitor, current leads voltage.

• Inductive reactance increases with frequency, while capacitive reactance decreases.

When both are present in a circuit, their effects can even cancel each other out — a concept known as resonance.

---

🔚 Conclusion

Reactance is a fundamental concept that explains how inductors and capacitors behave in AC circuits. Unlike resistance, which simply dissipates energy, reactance arises because energy is temporarily stored and returned through magnetic and electric fields.

Inductive reactance opposes changes in current, while capacitive reactance opposes changes in voltage. Their frequency-dependent nature allows engineers to design filters, oscillators, tuned circuits, and frequency-selective systems.

Understanding reactance is a crucial step toward mastering AC circuit analysis and leads naturally into deeper topics like impedance, resonance, and AC power systems.

Understanding Inductors and Inductance — How Magnetic Energy Is Stored

In electronic circuits, not all components respond instantly to changes. Some store energy and react over time. One such fundamental component is the inductor, which stores energy in a magnetic field and resists changes in current.

In this blog, we’ll understand what an inductor is, how it works, how it stores energy, and what inductance really means.

---

⚙️ What is an Inductor?

An inductor is a passive electronic component that stores electrical energy in the form of a magnetic field.
It mainly opposes changes in current — just like a capacitor opposes changes in voltage.

Whenever current starts flowing through an inductor, it generates a magnetic field around it.
And when that current changes (increases or decreases), the magnetic field changes too — which in turn induces a voltage that tries to oppose that change.

That’s the fundamental nature of an inductor.

---

🧱 Structure — How It’s Made

An inductor is typically made of:

1. A coil of wire — usually copper, wound in loops or turns.

2. A core — which can be air, iron, or ferrite placed inside the coil to enhance its magnetic properties.

3. Two terminals / leads — for connection to the circuit.

The more turns the coil has, and the better the core material, the stronger the magnetic field it can create — and hence, the higher the inductance.

---

⚙️ How Does an Inductor Work?

Before any current flows:

• There is no magnetic field around the coil.

When a voltage source is connected:

1. Current starts flowing through the wire coil.

2. As current flows, a magnetic field forms around the coil (according to Ampere’s Law).

3. If the current keeps increasing, the magnetic field grows — but this change in magnetic flux induces an opposing voltage (back EMF) in the coil (as per Faraday’s Law of Electromagnetic Induction).

4. This induced voltage always acts in the opposite direction of the applied voltage — this is Lenz’s Law in action.

So what’s happening inside is that the inductor resists any change in current.

• If you try to increase current, it generates a voltage that opposes the increase.

• If you try to decrease current, it generates a voltage that tries to keep it flowing.

---

💡 In Simple Words

• Capacitor → opposes change in voltage

• Inductor → opposes change in current

---

🔋 Energy Storage in an Inductor

An inductor stores energy in the magnetic field created by the current flowing through it.

The moment you disconnect the source, this magnetic field collapses and releases energy back into the circuit.

The energy stored is given by:

E = ½ L I²

where:

• E = energy stored (joules)

• L = inductance (henries, H)

• I = current through the inductor (amperes)

Just like a capacitor stores energy in an electric field, an inductor stores it in a magnetic field.

---

🧮 What is Inductance?

Inductance is the ability of an inductor to store magnetic flux per unit current.

In simple terms, it tells how much magnetic field (or magnetic flux) an inductor can produce for a given current flowing through it.

It is denoted by L and measured in Henries (H).

Mathematically:

L = NΦ / I

where:

• N = number of turns in the coil

• Φ = magnetic flux linked with the coil (Weber)

• I = current through the coil (amperes)

It basically tells us how much magnetic flux is produced for a given current.

---

⚡ Voltage–Current Relationship

The voltage across an inductor is given by:

V = L (dI/dt)

This means:

• If the current changes rapidly, the induced voltage is large.

• If the current is steady, dI/dt = 0, so the voltage across the inductor is zero.

Once fully energized with DC, an inductor behaves like a short circuit.

---

🧠 Factors Affecting Inductance

1. Number of Turns (N): More turns → higher inductance

2. Core Material: Iron or ferrite cores concentrate magnetic flux → higher inductance

3. Cross-sectional Area (A): Larger area → stronger field → higher inductance

4. Length of Coil (l): Longer coil → weaker field → lower inductance

For a solenoid:

L = (μ N² A) / l

where:

• μ = permeability of the core material

• N = number of turns

• A = cross-sectional area

• l = length of the coil

Here, μ (mu) plays a similar role as ε (epsilon) in capacitors — it tells how well the core supports the magnetic field.

---

🧩 Summary Table

---

🔚 Conclusion

An inductor is a fundamental passive component that stores energy in the form of a magnetic field and resists changes in current. By generating an opposing voltage whenever current changes, inductors play a critical role in controlling current flow in electronic circuits.

Inductance defines how effectively an inductor can store magnetic energy, and it depends on physical factors like the number of turns, core material, and coil geometry. Inductors are widely used in filters, power supplies, energy storage systems, and signal processing circuits.

Understanding inductors and inductance provides a strong foundation for learning AC circuits, RL circuits, transformers, and advanced analog electronics.

Understanding Capacitors and Capacitance — How Electrical Energy Is Stored

 In electronic circuits, energy is not only consumed — it can also be temporarily stored and released when needed. One of the most important components that makes this possible is the capacitor.

In this blog, we’ll understand what a capacitor is, how it works, how it stores energy, and what capacitance really means.

---

⚙️ What is a Capacitor?

A capacitor is an electronic component that stores electrical energy in the form of an electric field.

---

🧩 Structure — How It’s Made

A basic capacitor consists of three parts:

1. Two Conducting Plates – usually made of metal like aluminum or copper.

2. Dielectric Material – an insulating layer placed between the plates (air, paper, plastic, ceramic, or mica).

3. Leads / Terminals – used to connect the capacitor into a circuit.

So physically, a capacitor looks like two metal plates separated by a thin insulating film.

The dielectric does not conduct electricity — it helps store charge by preventing electrons from jumping directly from one plate to the other.

---

⚡ How Does a Capacitor Work?

Before applying voltage:

• Both plates are electrically neutral, meaning they have an equal number of positive and negative charges.

After connecting the capacitor to a battery:

1. The negative terminal of the battery pushes electrons toward the bottom plate of the capacitor through the connecting wire.
   → This bottom plate starts accumulating extra electrons and becomes negatively charged.

2. As electrons pile up on the bottom plate, they repel electrons from the top plate (because like charges repel).

3. These repelled electrons from the top plate move through the external circuit toward the positive terminal of the battery, which is electron-deficient and attracts them.

4. The top plate, having lost electrons, becomes positively charged.

Meanwhile, the dielectric between the plates prevents direct electron flow — it only allows an electric field to form.

As charge separation builds up, a potential difference (voltage) develops across the plates.
This continues until the voltage across the capacitor equals the battery voltage — at that point, charging stops.

The electric field created between the plates stores the electrical energy.

The electric field strength is given by:

E = V / d

where:

• V = voltage across the plates

• d = distance between the plates

---

🔋 Energy Storage in a Capacitor

The capacitor now holds energy in the electric field between its plates.

If the battery is disconnected, the charges remain stored — the capacitor stays charged.

It releases this stored energy only when a conductive path (like a resistor or load) is connected between its plates.
Electrons then flow from the negatively charged plate to the positively charged plate through the external circuit, producing current until both plates become neutral again.

This process is called discharging the capacitor.

---

🧮 What is Capacitance?

Capacitance is the ability of a capacitor to store electric charge per unit voltage.

In simple terms, it tells how much charge a capacitor can store for a given applied voltage.

Mathematically:

C = Q / V

where:

• C = capacitance (Farads, F)

• Q = charge stored (Coulombs)

• V = voltage across the capacitor (Volts)

A higher capacitance means greater charge storage capability.

---

⚡ Current–Voltage Relationship in a Capacitor

The relationship between current and voltage for a capacitor is:

I = C (dV/dt)

This means:

• If voltage changes rapidly, current is large.

• If voltage is constant, current is zero.

So a capacitor allows current to flow only when voltage is changing.
A capacitor opposes sudden changes in voltage.

---

🧠 Factors Affecting Capacitance

1. Area of Plates (A): Larger area → more charge → higher capacitance

2. Distance Between Plates (d): Greater distance → lower capacitance

3. Dielectric Constant (ε): Better dielectric → higher capacitance

For a parallel plate capacitor:

C = ε (A / d)

From this:

• Bigger plates → higher capacitance

• Closer plates → higher capacitance

• Better dielectric → higher capacitance

---

🔥 Energy Stored in a Capacitor

The energy stored in a capacitor is given by:

E = (1/2) C V²

---

🔚 Conclusion

A capacitor is a fundamental electronic component that stores electrical energy in the form of an electric field. By separating charge across two plates using a dielectric, it plays a crucial role in energy storage, voltage stabilization, filtering, timing circuits, and signal coupling.

Capacitance defines how effectively a capacitor can store charge, and it depends on the physical structure and dielectric material used. Capacitors respond to changes in voltage rather than steady values, which makes them essential in both analog and digital electronics.

Understanding capacitors and capacitance lays a strong foundation for learning RC circuits, filters, power supplies, and advanced analog electronic systems.